This module assumes that the virtual battery will be operated to participate in the hourly energy market. Currently, both hourly energy prices and hourly balancing prices are accepted by the algorithm, which is detailed below. The optimization routine that approximates dispatch for the virtual battery is the same used in the energy storage market participation module.
The Market Participation algorithm is based on the linear program proposed in [1], but generalized to accommodate a virtual battery. It outputs the optimal power exchange between the energy storage asset and grid, and uses this result to determine a modified load profile as well as the applicable energy costs with and without the energy storage. The modified load profile can then be used to quantify other project impacts.
For more information on the virtual battery model, see the virtual battery documentation.
Optimization Algorithm
Variable Definitions
\(P^{inj}_k\): Power injected into the grid
\(P^{with}_k\): Power withdrawn from the grid
\(X_k\): Virtual battery charge
\(r^{+}_k\): Balancing up capacity
\(r^{-}_k\): Balancing down capacity
Parameter Definitions
\(\overline{P}^{inj}_k\): Maximum injection power
\(\overline{P}^{with}_k\): Maximum withdrawal power
\(\overline{X}_k\): Maximum charge
\(\underline{X}_k\): Minimum charge
\(X_{final}\): Required final charge
\(\lambda_k\): Energy price
\(\beta^{+}_k\): Balancing up price
\(\beta^{-}_k\): Balancing down price
\(\eta_{inj}\): Injection efficiency
\(\eta_{with}\): Withdrawal efficiency
\(\alpha\): Self-discharge
Objective Function
\( \min \sum \limits_{k} \lambda_k \left( P_{with} – P_{inj} \right) – \beta^+_k r^+_k – \beta^-_k r^-_k \)
Constraints
\( X_{k+1} = \alpha X_k + \eta_{with} P^{with}_k – \frac{1}{\eta_{inj}} P^{inj}_k \qquad \forall k \)
\( 0 \leq P^{inj}_k \leq \overline{P}^{inj}_k \qquad \forall_k \)
\( 0 \leq P^{with}_k \leq \overline{P}^{with}_k \qquad \forall_k \)
\( \underline{X}_k \leq X_k \leq \overline{X}_k \qquad \forall_k \)
\( X_K = X_{final} \)
\( r^+_k \leq \overline{P}^{inj}_k – P^{inj}_k + P^{with}_k \qquad \forall_k \)
\( r^-_k \leq P^{inj}_k – P^{with}_k + \overline{P}^{with}_k \qquad \forall_k \)
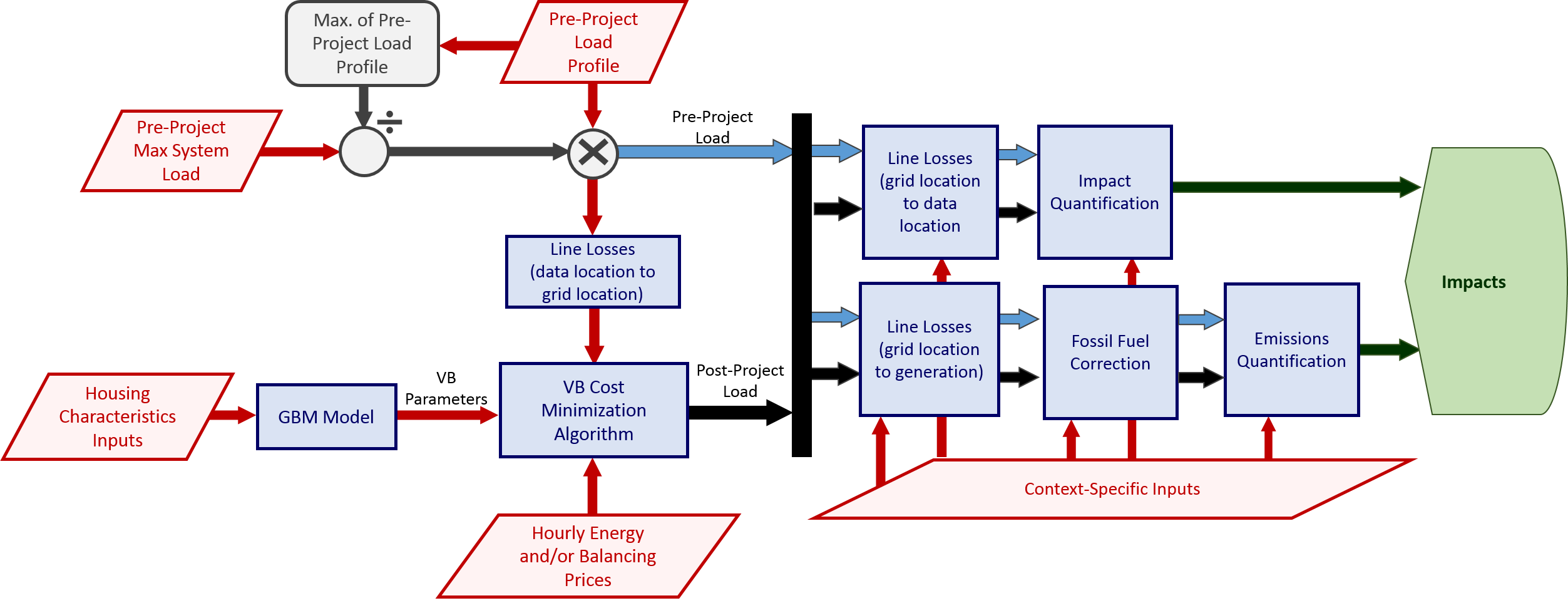
The flowchart below illustrates how this module is used within the context of a GridPIQ project. The market participation calculation is signified by the box labeled “VB Cost Minimization Algorithm”.
References
1. Wu D, C Jin, PJ Balducci, and MCW Kintner-Meyer. 2015. “An Energy Storage Assessment: Using Optimal Control Strategies to Capture Multiple Services.” In IEEE Power and Energy Society General Meeting, July 26-30, 2015, Denver, Colorado, pp. 1-5. IEEE, Piscataway, NJ. doi:10.1109/PESGM.2015.7285820
