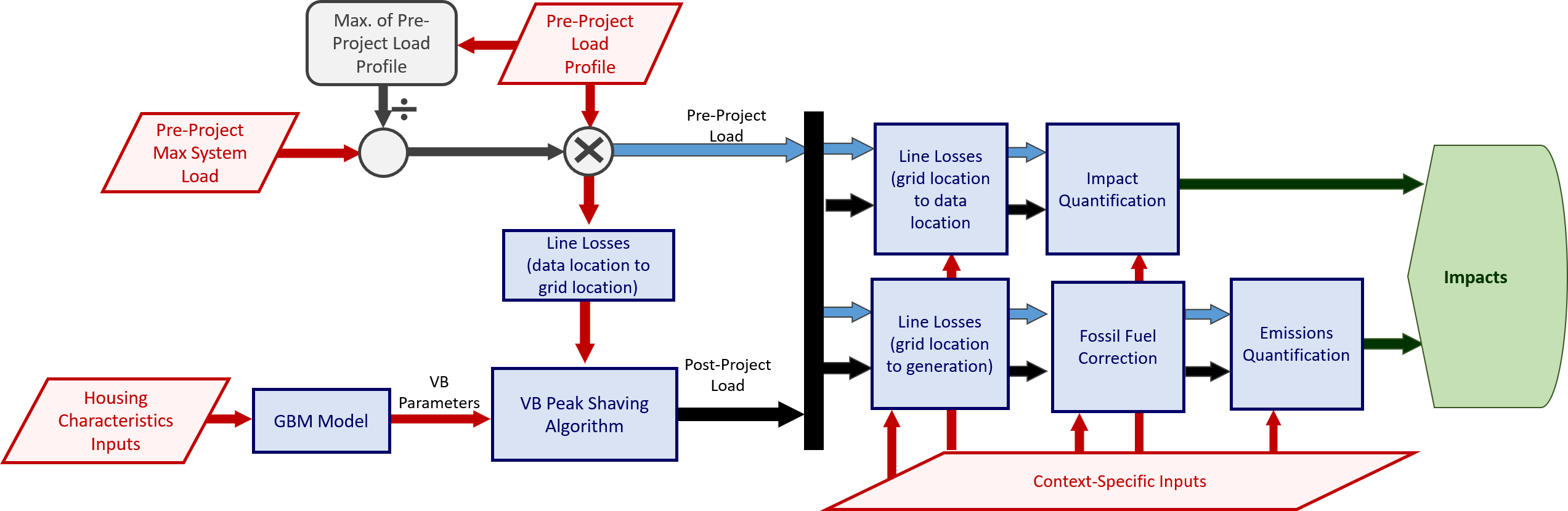
This module assumes that the virtual battery will be operated with the objective of shaving peaks and filling valleys in the overall load profile. The optimization routine that estimates dispatch for the virtual battery is a generalization of the routine used in the energy storage daily peak reduction module.
The daily peak reduction algorithm seeks to minimize the sum of squared post-project load for each hour in the optimization window. This results in peak reduction because it drives the load away from especially large loads (their impacts are amplified by squaring), while also discouraging increases in total load that would come from heavy battery usage. It outputs the optimal power exchange between the energy storage asset and grid, and uses this result to determine a modified load profile that is used to quantify project impacts.
To speed up computation time, the total time period input by the user is split up into weekly intervals and the optimization routine is solved iteratively over these intervals.
For more information on the virtual battery model, see the virtual battery documentation.
Optimization Algorithm
Variable Definitions
\(P^{inj}_k\): Power injected into the grid
\(P^{with}_k\): Power withdrawn from the grid
\(X_k\): Virtual battery charge
Parameter Definitions
\(L_k\): Pre-project load
\(\overline{P}^{inj}_k\): Maximum injection power
\(\overline{P}^{with}_k\): Maximum withdrawal power
\(\overline{X}_k\): Maximum charge
\(\underline{X}_k\): Minimum charge
\(X_{final}\): Required final charge
\(\eta_{inj}\): Injection efficiency
\(\eta_{with}\): Withdrawal efficiency
\(\alpha\): Self-discharge
Objective Function
\( \min \sum \limits_{k} \left( L_k + P^{with}_k – P^{inj}_k \right)^2 \)
Constraints
\( X_{k+1} = \alpha X_k + \eta_{with} P^{with}_k – \frac{1}{\eta_{inj}} P^{inj}_k \qquad \forall k \)
\( 0 \leq P^{inj}_k \leq \overline{P}^{inj}_k \qquad \forall_k \)
\( 0 \leq P^{with}_k \leq \overline{P}^{with}_k \qquad \forall_k \)
\( \underline{X}_k \leq X_k \leq \overline{X}_k \qquad \forall_k \)
\( X_K = X_{final} \)
The flowchart below illustrates how this module is used within the context of a GridPIQ project. The daily peak reduction calculation is signified by the box labeled “VB Peak Shaving Algorithm”.