The Market Participation objective assumes that a new energy storage system will be operated to maximize economic benefit based on hourly price signals. The objective module has been implemented as a linear programming (LP) algorithm and is derived from work done by Wu (2015). Implicit in this implementation is that operation of the energy storage system does not change dispatch or alter the price of energy.
A process flow diagram illustrating how the objective module operates within the larger context of the tool is provided below.
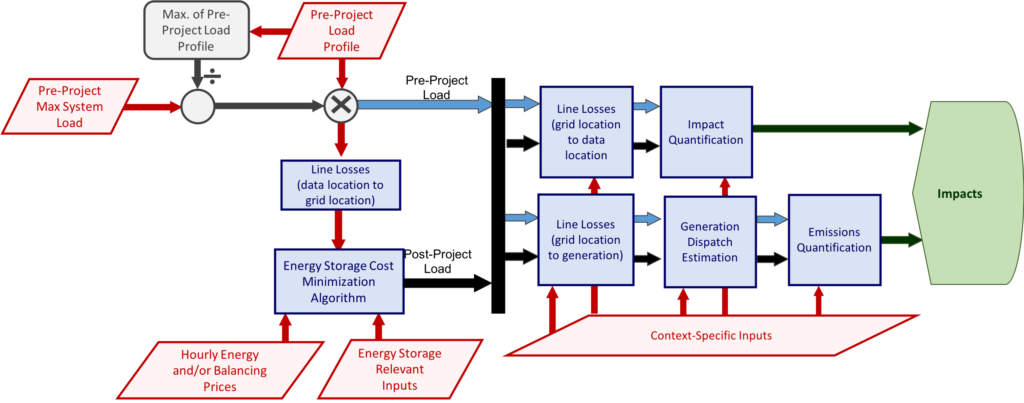
Energy Storage System Specifications
The specifications of any energy storage project generally include power and energy ratings. The power rating, specified here in megawatts (MW), determines the rate of transfer of energy that can be supplied or consumed per unit of time. A system with a higher power rating can charge or discharge quicker than one with a lower power rating. The energy capacity, specified in megawatt-hours (MWh), determines the total amount of energy that the system is able to store or deliver over time. The energy to power ratio (E/P) indicates the time duration (in hours, minutes or seconds) that the system can operate while delivering its rated output. For example, a lithium-ion battery with a power rating of 32MW, and an energy capacity of 8MWh, can deliver power for 15 minutes when discharging at its rated value.
The power and energy requirements may be different based on the target applications. If the primary function of the system is to provide frequency regulation, a higher power rating is preferred so that the system can charge and discharge frequently over a short duration of time. On the other hand, if the primary function is to enable peak-shifting or provide backup power in case of outage, the energy rating will be higher so that the battery can deliver power over a longer time.
Within the context of the optimization algorithm, operation of the energy storage technology is constrained to ensure that its resulting discharge and charge behavior does not occur at a rate exceeding the power capacity defined by the user. Similarly, the user-supplied energy capacity dictates the maximum amount of energy that the system can store when it is fully charged. These values are provided by users in MW and MWh respectively.
The algorithm treats the energy capacity value as usable energy, assuming that the energy storage system can be discharged down to a 0% state of charge and charged to 100%, which may be different than the system’s actual operating parameters. As an example, if the storage system can only be operated between 20% and 100% of its nominal energy capacity, the energy capacity value should be derated to 80% when entered into the tool.
The round trip efficiency (RTE) of an energy storage system is defined as the ratio of the total energy output by the system to the total energy input to the system, as measured at the point of connection. The RTE varies widely for different storage technologies. A high value means that the incurred losses are low.
Price Data
Currently, the Market Participation algorithm will accept two types of price information: the hourly price of electrical energy and the hourly value of balancing capacity. Each of these sets of price data must be provided to the tool as comma-separated values (CSV).
Energy price information will drive the operation of the energy storage system toward arbitrage or economic dispatch, where the benefit to the project owner is the difference in energy price during periods of buying (ESS charging) and selling (ESS discharging) minus the cost of losses. Energy price data should be provided in dollars per megawatt-hour ($/MWh) for each hour of the load period.
Balancing prices represent the value in each hour of reserved energy capacity to either absorb excess generation (balancing down) or to serve unmet load (balancing up). These balancing up and balancing down prices should be provided in dollars per megawatt ($/MW) for every hour of the load period. In the absence of balancing signals, this algorithm reserves the necessary capacity to perform this balancing service when it is economically advantageous, but assumes that balancing actions taken are energy neutral within the hour.
Algorithm Outputs
The Market Participation algorithm outputs a modified load profile as well as the applicable energy costs with and without the energy storage system. The modified load profiles can then be used to quantify other project impacts.
Optimization Algorithm
The optimization routine has been implemented in Python using the package pyomo and the solver, ipopt, using its default parameters.
To reduce runtime, load periods that exceed the length of a leap year are divided evenly into segments of no longer than 8784 hours. If there is an hour remaining after the division, it is added to the final segment. The optimization routine then operates independently on each segment of the complete project load profile. The energy storage system’s state of charge is 0% when the optimization begins, and it is constrained to empty at the end of each optimization period.
The tool assumes that regional demand should never be allowed to go negative. The ESS is therefore never permitted to discharge such that the post-project load profile would dip below zero.
Variable definitions
\(p\): Power transfer between the ESS and the grid
\(p_{inj}\): Power injected into the grid by the ESS
\(p_{with}\): Power withdrawn from the grid by the ESS
\(P_{inj,max}\): Maximum ESS injection power
\(P_{with,max}\): Maximum ESS withdrawal power
\(\lambda\): Hourly energy price
\(\beta^{+}\): Balancing up price
\(\beta^{-}\): Balancing down price
\(r^{+}\): Balancing up capacity
\(r^{-}\): Balancing down capacity
\(\eta_{rt}\): Round-trip efficiency
\(\eta^{+}\): Charge efficiency
\(\eta^{-}\): Discharge efficiency
\(E_{s}\): ESS energy capacity
\(SoC\): ESS state of charge
\(SoC_{min}\): Minimum ESS state of charge
\(SoC_{max}\): Maximum ESS state of charge
\(L\): Pre-project electrical load
\(K\): Total number of hours in the optimization period
\(\Delta t\): Elapsed time between steps (here one hour)
Where:
\(p = p_{with} – p_{inj}\)
\(SoC_{k} = SoC_{k-1} + eta^{+} p_{with} – \frac{p_{inj}}{eta^{-}}\)
\(eta^{+} = eta^{-} = \sqrt{eta_{rt}}\)
In the implementation of the algorithm within the context of the website’s user interface, several additional assumptions are made. The charge and discharge efficiency values are assumed to be equal as well as the maximum charge and discharge powers. Additionally, the ESS is completely empty at the beginning of each optimization period and the algorithm enforces 0% state of charge at the end of the period. Finally, the minimum state of charge is zero and the maximum is the user-defined energy capacity.
\(P_{inj,max} = P_{with,max}\)
\(SoC_{1} = SoC_{K} = 0\)
\(SoC_{min} = 0\)
\(SoC_{max} = E_{s}\)
Objective function:
\(min\sum \lambda p + \beta^{+} r^{+} + \beta^{-} r^{-}\)
Subject to:
Power injection limits: \(0 \leq p_{inj} \leq P_{inj,max}\)
Power withdrawal limits: \(0 \leq p_{with} \leq P_{with,max}\)
Load limits: \(p_{inj} – p_{with} <= L\)
State of charge limits: \(SoC_{min} \leq SoC \leq SoC_{max}\)
r(+) up capacity: \(r^{+} \leq P_{inj,max} – p\)
r(-) down capacity: \(r^{-} \leq P_{with,max} + p \)
SoC limits with balancing up: \(SoC_{min} \leq SoC – \frac{r^{+} \Delta t}{ \eta^{+} E_{s}} \leq SoC_{max}\)
SoC limits with balancing down: \(SoC_{min} \leq SoC + \frac{r^{-} \eta^{-}\Delta t} {E_{s} }\leq SoC_{max}\)
Reference
Wu D, C Jin, PJ Balducci, and MCW Kintner-Meyer. 2015. “An Energy Storage Assessment: Using Optimal Control Strategies to Capture Multiple Services.” In IEEE Power and Energy Society General Meeting, July 26-30, 2015, Denver, Colorado, pp. 1-5. IEEE, Piscataway, NJ. doi:10.1109/PESGM.2015.7285820
